Figure 2
* * * * *
Lorsqu'un coût de revient est le résultat d'un tel calcul, il demande donc des ventilations dans l'espace, en plus des ventilations dans le temps nécessitées par le découpage en périodes.
Ces ventilations dansl'espace peuvent s'opérer de multiples façons, qui peuvent se ranger en deux grandes catégories : coûts de revient complets ou coûts de revient partiels.
Pour un bien donné, un calcul de coût de revient peut donc fournir des réponses variées, sans qu'il soit possible d'affirmer qu'aucune constitue la bonne évaluation de son coût.
a) Coût de revient du produit
Le coût de revient d'un produit ou d'un service est défini, en comptabilité, comme "tout ce qu'a coûté" ce bien ou ce service. Or, dans le cas d'une entreprise produisant un seul produit, le compte de résultat fournit directement une telle évaluation.
Le compte de résultat peut être résumé en effet de la manière suivante :
résultat = ventes + augmentation des stocks - (charges + diminution des stocks)
ce qui s'écrit encore, compte tenu de la définition du coût de revient :
résultat = ventes + coût de revient des quantités stockées
- coût de revient des quantités produites
= ventes - coût de revient des quantités vendues.
Par exemple, le coût de revient des ventes de l'année, pour l'entreprise dont le compte de résultat figure chapitre III §II, s'établit de la manière suivante :
achats (300 + 200) 500
diminution de stocks 150
impôts et taxes 200
personnel 1 600
amortissements 300
provisions 90
charges financières 50
_______
total 2 890
moins :
augmentation des stocks - 290
________
coût de revient 2 600
Si, au cours de l'année, l'entreprise a vendu 1 000 unités de son produit supposé unique, on dit que le coût de revient moyen de chaque unité a été :
2 600 ----- = 2,60 1 000
Un usage courant d'un tel résultat est une comparaison avec le prix de vente : on sait que si l'on a vendu le produit à un prix supérieur à ce coût de revient, le résultat est positif aux charges et produits exceptionnels près.
Par ailleurs, on peut ainsi calculer l'incidence sur le coût de revient d'une augmentation générale des salaires ou des taxes.
Il arrive que l'on considère que le calcul du coût de revient une seule fois par an est une donnée insuffisante ; il peut alors être fait plus fréquemment, tous les mois, toutes les semaines, ou tous les jours. mais on voit alors la nécessité des ventilations dans le temps, pour que les oscillations du coût de revient restent interprétables : si, par exemple, on imputait intégralement une grosse réparation de machine à la semaine où elle a eu lieu, les résultats de cette semaine-là ne pourraient guère être comparés à ceux des autres.
Nous reviendrons, à la fin du présent chapitre, sur les conséquences des ventilations dans le temps sur le calcul des coûts de revient. Notons pour l'instant qu'elles sont le seul facteur conventionnel qui intervienne dans le calcul du coût de revient d'un produit unique, lorsqu'on ne s'intéresse qu'aux charges par natures.
b) Coûts comptables par fonctions
Supposons que l'entreprise assure elle-même la livraison par camions de son produit unique. Le chef d'entreprise peut se préoccuper du prix qu'il doit demander à ses clients pour ce service, et par conséquent, il veut connaître le coût du transport. Autre hypothèse : les chauffeurs de camions réclament une augmentation de salaires : le chef d'entreprise désire évidemment évaluer l'incidence d'une telle augmentation sur le coût de revient.
Le coût de revient du produit ne permet pas de répondre directement à de telles questions, car les charges y sont enregistrées comme dans le compte de résultat sans distinguer finement leur destination : tous les salaires par exemple, sont portés indistinctement dans la même rubrique.
Il est évidemment possible, pour répondre aux deux questions ci-dessus, de chercher dans toutes les charges celles qui sont dues à l'activité de transport et, dans tous les salaires, ceux qui sont versés aux chauffeurs de camions. Compte tenu de la manière dont les charges sont enregistrées en comptabilité générale, de telles opérations (appelées, de façon pittoresque, "débobinages des coûts de revient" par les comptables) sont laborieuses.
Il est jugé préférable, si l'on est amené à se poser fréquemment des questions de ce type, d'enregistrer directement les charges, non seulement par natures, mais par fonctions. On peut imaginer, dans l'entreprise considérée ici, trois fonctions : la direction, la production, et le transport. La comptabilité pourrait alors être résumée selon un tableau tel que le suivant :
direction production transport salaires ......... .......... ......... fournitures ......... .......... ......... amortissements ......... .......... ......... __________ __________ _________ ......... .......... .........
On a ici un premier exemple de comptabilité analytique. Tout se passe comme si les colonnes de ce tableau représentaient la partie "charges" des comptes de résultat de trois entreprises distinctes.
On aperçoit déjà sur ce cas simple qu'il peut y avoir de nombreuses variantes de comptabilités analytiques pour cette même entreprise. Si le salaire des chauffeurs de camions revient sans aucun doute au transport, en est-il de même des charges de manutention, par exemple, ou faut-il les imputer à la production ? Il sera tranché dans un sens ou dans l'autre et, si le but est seulement de permettre des comparaisons dans le temps, peu importe la convention adoptée, à condition que l'on s'y tienne.
Il se pose de nombreux problèmes de répartition et d'imputation de ce genre dans toute comptabilité analytique. Ce qu'il importe d'en retenir, c'est que selon les règles adoptées, le coût comptable du transport, par exemple, aura une valeur, un contenu et une signification variables. Comme notre préoccupation est l'évaluation des dépenses effectives, qui ne dépendent évidemment pas de ces conventions, nous avons déjà là un exemple des ventilations dans l'espace qui affectent les coûts comptables, en plus des ventilations dans le temps évoquées précédemment.
Néanmoins, dans le cas d'un produit unique considéré jusqu'ici, il ne se pose pas de problème de ventilation dans l'espace pour le coût de revient du produit lui-même, mais seulement pour le coût comptable des fonctions qui concourent à sa production.
Il n'en va plus de même lorsque l'entreprise fabrique plusieurs produits.
a) Position du problème
Pour une usine vendant différents objets ou services, la rémunération du directeur général a bien pour raison d'être ces fabrications, et les prix de vente doivent sans doute couvrir cette charge comme les autres, mais il est permis de se demander quelle part de cette rémunération est imputable à chaque production.
Le problème se complique encore lorsque l'on s'intéresse aux coûts des services que les différents organes de la maison se prêtent les uns aux autres, surtout lorsque ces services sont réciproques. Par exemple, le service des transports travaille pour le service du matériel, et le service du matériel pour le service des transports. Le coût de chacun de ces services est fonction du coût de l'autre.
Dans le cas du produit unique, le choix des ventilations était sans conséquence sur le coût de revient du produit. Au contraire, il est déterminant dans le cas de plusieurs produits, si la fabrication de ceux-ci fait inégalement appel aux différents services internes.
Nous allons montrer comment dans ce cas les coûts comptables sont établis grâce à l'introduction de différentes notions comptables.
b) Centres de coûts, unités d'oeuvres, clefs de répartition
On définit, au sein de l'entreprise, un certain nombre de sous-ensembles, appelés centres de coûts (ou sections), qui ont pour caractéristiques de fournir des biens ou des services qui puissent être considérés comme des multiples d'une unité déterminée, appelée unité d'oeuvre. Pour un centre de production, l'unité d'oeuvre sera le produit fabriqué. Pour un centre de transport, ce pourra être la TKU (tonne x km utile), etc.
On s'efforce de faire en sorte qu'un centre de coût corresponde à une unité de responsabilité, mais ce n'est pas toujours possible. Par exemple, on peut définir un centre "bâtiments", dont l'unité d'oeuvre pourra être le mètre carré occupé.
Les centres de coûts permettent ainsi de prendre en compte les charges qu'on ne peut pas affecter sans ambiguïté à un produit et qui sont appelées charges indirectes (par opposition aux charges directes).
Certaines charges de frais généraux ne sont pas prises en compte par un centre, mais ventilées entre les centres en fonction de règles simples, par exemple au prorata de leurs charges propres. On appelle ces règles des clefs de répartition.
A l'aide de ces différents concepts, il devient possible de décrire fictivement l'entreprise comme un ensemble de centres de production qui se rendent des services, moyennant paiement à leur coût comptable des unités d'oeuvre consommées, en sorte que chaque centre équilibre ses "recettes" et ses "dépenses".
Nous allons montrer sur un exemple comment ces calculs peuvent être conduits, grâce à l'hypothèse de proportionnalité des quantités d'unités d'oeuvres et des frais qui fonde les divers concepts énumérés.
c) Calcul des coûts de revient complets
Bien que les comptables ne le formalisent généralement pas ainsi, comme nous l'expliquerons, nous présenterons le calcul des coûts de revient sous une forme algébrique.
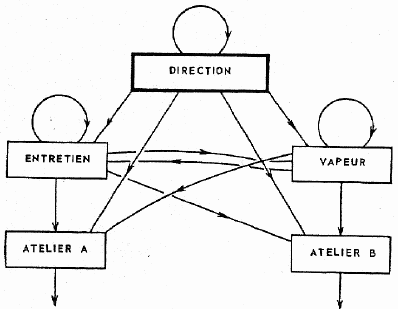
Pour fixer les idées, nous considérons une entreprises chématisée par le graphe de la figure 2.
Une flèche signifie que la section située à l'origine rend des services à la section située à l'extrémité.

Figure 2
Notations
coût comptable des unités d'oeuvre (inconnues) :
F (comme frais généraux): unité d'oeuvre
de la direction,par exemple l'unité
de charges propres et directes des sections.
V unité d'oeuvre de l'atelier devapeur,
par exemple le kg de vapeur.
E unité d'oeuvre de l'atelierd'entretien,
par exemple l'heure d'ouvrier.
A coût de revient du produit A.
B coût de revient du produit B.
charges propres :
D(f) charges propres de la direction.
D(v) charges propres de l'atelier de vapeur.
D(a) charges propres de l'atelier A = charges directes du produit A.
etc.
nombre d'unités d'oeuvres :
f nombre d'unités d'oeuvre fournies par la direction.
v nombre de kg de vapeur.
a production du produit A.
etc.
prestations :
v(e) nombre de kg de vapeur fournis à l'entretien.
e(v) nombre d'heures d'entretien fournies à l'atelier de vapeur.
f(a) nombre d'unités de frais généraux consommées
par l'atelier A.
etc.
On peut ainsi définir les unités d'oeuvre fournies par
un service à lui-même, par exemple ici : e(e) nombre
d'heures d'entretien consommées par le service d'entretien,
f(f) nombre d'unités de frais généraux consommées
par la direction générale pour son propre fonctionnement.
On a évidemment : e = SIGMA e (i) par exemple.
Écrivons l'équilibre des consommations et des productions de chaque service :
direction : D (f) + f (f) F = fF entretien : D (e) + e (e) E + f (e) F + v(e) V = eE vapeur : D (v) + e (v) E + f (v) F + v(v) V = vV atelier A : D (a) + e (a) E + f (a) F + v(a) V = aA atelier B : D (b) + e (b) E + f (b) F + v(b) V = bBCe système peut s'écrire, sous forme matricielle :
-f+f(f) 0 0 0 0 F - D (f)
f(e) -e+e(e) v(e) 0 0 E - D (e)
f(v) e(v) -v+v(v) 0 0 x V = - D (v)
f(a) e(a) v(a) -a 0 A - D (a)
f(b) e(b) v(b) 0 -b B - D (b)
soit : (matrice de répartition) x (vecteur des coûts de revient complets) = - (vecteur des charges propres).
Sous cette forme, le calcul des coûts de revient sera mène donc à la résolution d'un système linéaire, c'est-à-dire à l'inversion d'une matrice.
En fait, il est possible de pousser l'analyse plus loin, en remarquant qu'il peut être utile de décomposer les charges propres par natures (salaires, fournitures, etc.) et par conséquent d'obtenir les coûts comptables d'unités d'oeuvre décomposés par natures également.
On obtient alors une équation matricielle complète : (matrice de répartition) x (matrice des coûts comptables) = -(matrice des charges propres).
Dans des entreprises importantes, ce système peut être très volumineux (400 x 400 par exemple).
d) Définition du coût de revient complet
Les modalités de calcul des coûts de revient complets nous permettent d'en donner à présent une définition plus précise que celle qui figure dans le Plan comptable général.
On appelle coût de revient complet d'un bien ou d'un service le quotient, par le nombre d'unités produites au cours de l'exercice comptable considéré, de la part des charges du compte de résultat de ce même exercice ventilée conventionnellement sur ce bien ou ce service.
Pour celui qui veut évaluer le coût d'une décision, une comptabilité analytique complète présente le danger de donner l'apparence de répondre à la plupart des questions qu'il se pose sur les coûts. Si un projet prévoit entre autres des transports, de l'entretien et de la fourniture de vapeur, la tentation est grande de calculer le nombre d'unités d'oeuvre correspondantes, et de multiplier par le coût comptable de chaque unité d'oeuvre. Un tel calcul peut fortuitement donner satisfaction, mais il n' ya aucune raison a priori pour qu'il en soit ainsi, et cela pour différentes raisons.
a) Conséquences des ventilations
L'équation matricielle établit une interdépendance entre tous les coûts comptables. Par conséquent, une modification de l'un des facteurs directs dans un centre rejaillit sur tous les autres centres. Si, par exemple, l'atelier A diminue de façon importante ses charges directes, il absorbera moins de frais généraux, prestations de la Direction au reste de l'entreprise, qui sont ventilées, on l'a dit, au prorata des charges propres des centres. Comme on suppose que le total des frais généraux reste constant ainsi que les charges propres des autres sections, ceci entraînera une augmentation du coût comptable du kg de vapeur, de l'heure d'entretien, et du produit B, sans que rien n'ait changé dans les centres correspondants.
b) Hypothèse de proportionnalité
Comme il a déjà été indiqué, cette méthode repose sur l'hypothèse de la proportionnalité des coûts et des quantités, qui repose elle-même, comme on l'a dit, sur l'analogie entre le fonctionnement interne de l'entreprise et un marché quelconque. L'univers extérieur étant inchangé, une entreprise vend bien la dernière unité produite au même prix que la première, même si l'on a des raisons de penser que les coûts correspondants sont très différents.
Cela dit, même si les coûts de revient complets peuvent représenter de façon à peu près satisfaisante un phénomène moyen, ils peuvent être extrêmement faux dans des cas particuliers. Il est bien évident que dix heures d'entretien de suite n'ont pas de raison d'être équivalentes à une heure par jour pendant dix jours, compte tenu des problèmes de planification de l'atelier d'entretien.
De même, si l'atelier A réclame brusquement une quantité très importante de vapeur, cela peut gêner l'atelier B au point de coûter effectivement beaucoup plus cher au total que la simple facturation au kg.
On verra mieux au chapitre VII qu'une comptabilité, si perfectionnée soit-elle, est incapable de répondre complètement aux problèmes ainsi posés. Néanmoins, des développements modernes de la comptabilité analytique apportent des remè des à quelques-uns des défauts du calcul des coûts de revient complets. Nous en donnons un aperçu dans les pages qui suivent.
Pour l'instant, retenons que l'hypothèse de proportionnalité néglige une distinction essentielle : celle des frais fixes et des frais variables. Nous illustrerons l'un des dangers de cette simplification par un exemple chiffré.
Imaginons une entreprise, plus simple encore que la précédente (fig.3), limitée à trois unités : un centre de frais généraux, dont les dépenses ne dépendent pas des variations à court terme de l'activité, et deux ateliers A et B, dont les dépenses varient proportionnellement à la production. Soit, par exemple :
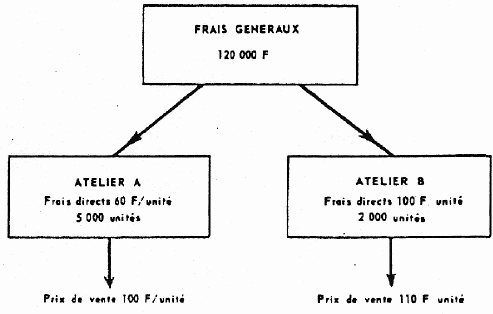
Figure 3
frais généraux : 120 000 F atelier A : frais directs variables : 60 F/unité ; production: 5 000 60 x 5 000 = 300 000 F atelier B : frais directs variables : 100 F/unité ; production: 2 000 100 x 2 000 = 200 000 F
et supposons que les frais généraux soient ventilés au prorata des frais directs, pratique très répandue dans l'industrie.
Il revient à chaque atelier :
300 000 3
___________________ = ___ pour A
300 000 + 200 000 5
et
200 000 2
___________________ = ___ pour B
300 000 + 200 000 5
On aura :
3
coût de revient de A = 300 000 + ___ x 120 000 = 372 000 F
5
2
coût de revient de B = 200 000 + ___ x 120 000 = 248 000 F
5
Supposons enfin que le produit A soit vendu 100 F, et le produit B, 110 F.
La vente de A rapporte : 500 000 F
La vente de B rapporte : 220 000 F
Il semble donc que l'entreprise gagne sur la vente de A :
500 000 - 372 000 = 128 000 F
et perde, sur la vente de B :
248 000 - 220 000 = 28 000 F
Il y a là une tentation de conclure qu'il faut renoncer au produit B.
Sur cet exemple schématique, on voit à l'évidence combien cette conclusion est fallacieuse.
En effet, la marge brute sur A, c'est-à-dire la différence entre ventes et frais variables, représente à elle seule 200 000 F, et elle permet de couvrir, et au-delà, tous les frais généraux. Par conséquent, la fabrication et la vente de B laissent une marge brute de : 220000 - 200 000 = 20 000 F et il n'y a pas de raison a priori de renoncer au produit B.
Nous voyons donc, sur cet exemple, l'intérêt que peut présenter la distinction entre frais fixes et frais variables, et un certain nombre de méthodes de comptabilité analytique mettent cette distinction en évidence.
Bien que cela ne fasse pas directement partie de notre propos, nous devons signaler ici un outil de réflexion souvent employé, qui exploite précisément cette distinction entre frais fixes et frais variables.
Sur un graphique portant en abscisse les quantités fabriquées, on porte en ordonnée la marge brute cumulée procurée par ces quantités, et d'autre part les frais fixes. La figure 4 représente un tel graphique avec les données du paragraphe précédent.
Le point d'intersection P est appelé "point mort". Son abscisse est théoriquement la production en deçà de laquelle l'entreprise est en perte.
Sous cette forme, ce graphique paraît à la fois bien élémentaire, et critiquable. En effet, en inversant l'ordre des produits, on trouverait un autre point mort P'. En fait, l'ordre adopté est fonction de la question que l'on se pose.
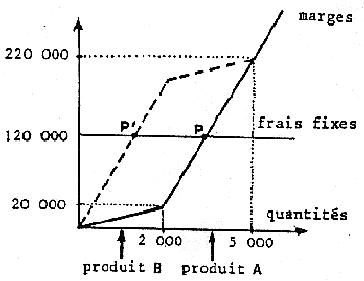
Figure 4
Par ailleurs, on peut noter que l'hypothèse de linéarité est d'un degré seulement moins sommaire que l'hypothèse de proportionnalité. Il faut cependant considérer que les raisonnements se font généralement au voisinage du point mort, et que, sur de petites variations, l'hypothèse de linéarité peut être légitime. En outre, il est loisible de considérer des seuils dans les frais fixes (investissements supplémentaires par exemple). Ainsi, dans le cas de la figure 5, il y a plusieurs points morts, et des fourchettes de production déficitaires, d'autres bénéficiaires.
On donne à ces méthodes un nom un peu optimiste: les analyses de rentabilité.
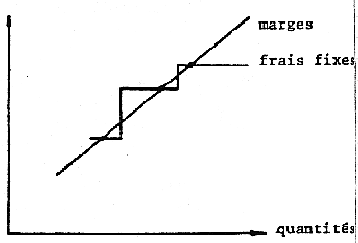
Figure 5
Cette présentation conduit à s'interroger sur la nature des frais fixes.
En fait, les frais fixes ne sont pas plus fixes que les autres. On en ferme simplement dans cette catégorie les frais qui ne sont pas directement influencés par les modifications particulières que l'on étudie. Autrement dit, ils ne sont pas définis dans l'absolu, et dépendent de l'ampleur des variations que l'on envisage, en volume et en durée.
En fait, les frais fixes habituellement considérés sont ceux que l'entreprise doit couvrir de toutes façons pour maintenir une structure pouvant fournir une activité "normale". Sont compris par exemple les amortissements des installations permanentes et les frais généraux qui ne sont pas influencés parl es variations à court terme de l'activité.
Il apparaît, dans ces conditions, que les frais fixes ne peuvent être définis avec précision qu'en fonction de la description des normes de marche de l'entreprise. Cette notion de norme joue un rôle central dans les différentes méthodes qui prennent en compte la distinction entre frais fixes et frais variables, et dont nous indiquons sommairement quelques exemples ci-après.
Considérons par exemple une entreprise qui a 1 000 de frais fixes, et 10 de frais variables par unité produite. L'un des inconvénients du coût de revient complet est qu'il varie avec la quantité produite N. Il vaut en effet :
1 000
10 + ________
N
Pour éviter cette variation, on définit l aproduction normale de l'entreprise pour la période considérée, par exemple 500 unités.
L'imputation rationnelle consiste à ajouter aux frais variables unitaires le total des frais fixes divisé par la production normale, ici 500, quelle que soit la production réelle de la période. Si par exemple cette production ne s'élève qu'à 400, et que tous les frais restent les mêmes, le coût de revient global calculé de cette manière s'élèvera à :
1000
400(10 + ________ ) = 400 x 12 = 4 800
500
Or, on a dépensé : 400 x 10 + 1 000 = 5000.
La différence : 200 est appelée : écart d'activité. L'idée centrale est que la structure de l'entreprise entraîne des dépenses dont la justification est une activité déterminée. Si cette activité n'est pas assurée, l'entreprise est temporairement ou durablement trop volumineuse, et l'imputation rationnelle permet de mettre en évidence de telles anomalies.
L'idée de norme, et d'écart par rapport à cette norme, que l'imputation rationnelle met en oeuvre, porte en germe l'idée d'une gestion qui ne porte son attention que sur les différences entre prévisions et réalisations. Compte tenu de la masse considérable de données que la comptabilité manipule, on entreprend ainsi de ne fournir à chaque responsable que des résultats qui requièrent son intervention : c'est le but du contrôle budgétaire.
On définit dans l'entreprise des centres de coûts qui se rapprochent plus des unités de commandement que des centres considérés ci-dessus.
Chaque centre de coût établit un "budget-programme", et un "budget des moyens", qui rassemblent respectivement les prévisions d'activité et les prévisions de dépenses pour la période suivante, par exemple le mois. Partant des centres de coûts élémentaires, les différents budgets sont discutés et synthétisés à chaque niveau hiérarchique, jusqu'à la Direction Générale.
Tous les éléments matériels et économiques du fonctionnement de l'entreprise étant ainsi prévus, il est alors possible de définir pour chaque bien ou opération un coût standard, qui représente ce que serait son coût de revient si tout se déroulait conformément aux prévisions.
Au moment où l'on dispose des résultats a posteriori, on calcule les différences avec les prévisions, et la considération des coûts standards permet, d'une part, d'analyser les écarts par natures à chaque niveau hiérarchique, et d'autre part, de les décomposer en écarts constatés à d'autres échelons.
Supposons que D désigne les charges d'un atelier x les frais fixes qui lui sont imputés y la quantité de produit entrant z le prix unitaire de ce produit t le nombre d'heures de travail u le prix de l'heure
Toutes ces données étant les standards retenus au début du mois, on constate à la fin du mois que les dépenses ont été en fait égales à D + dD.
Pour analyser les écarts par natures, on s'appuie sur la constatation suivante : si les quantités D, x, y, z, t, u sont reliées par la relation :
D = x + yz + tu
on doit avoir :
dD = dx + ydz + zdy + tdu + udt
On peut ainsi chiffrer chaque cause d'écart, en donnant aux autres variables leur valeur standard dans chaque terme.
Grâce à la formule précédente, il sera possible d'analyser cet écart global en :
dx : écart sur frais fixes ydz : écart sur prix des fournitures zdy : écart sur consommation etc.
Mais, de plus, chacun de ces écarts peut être à son tour analysé par d'autres services, en fonction de leurs responsabilités propres.
Par exemple, l'écart "du" sur le coût de l'heure de travail pourra être analysé par le service du personnel en écart sur salaire de base, écart par glissement catégoriel, écart sur primes, etc.
On peut imaginer de nombreuses variantes, et cet exemple suggère la fécondité de ces méthodes. Mais leur raffinement ne doit pas faire oublier le fait que, si elles permettent une appréciation des résultats passés, elles peuvent entretenir de dangereuses illusions sur le coût des décisions futures.
En effet, les coûts standards dans le cas considéré jusqu'ici ne sont jamais que des coûts de revient complets, et ils souffrent par conséquent des mêmes défauts. C'est ainsi que dans l'exemple précédent, les frais fixes x sont peut être le résultat d'investissements passés et de ventilations conventionnelles de frais généraux, dont le contrôle échappe au gestionnaire de l'atelier, et qui n'ont pas à intervenir dans ses décisions.
Il existe des méthodes de comptabilité analytique qui abandonnent le calcul des coûts de revient complets. Dans ces méthodes, on renonce en principe à toute ventilation arbitraire de frais indirects qui, n'étant pas affectables sans ambiguïté aux produits, sont comptabilisés uniquement au niveau où ils sont créés. De nombreuses variantes sont concevables à partir de ce principe et nous n'en donnerons ici qu'une illustration schématique.
Par exemple, supposons que l'entreprise soit composée d'un siège social et de plusieurs usines, elles-mêmes composées de services communs (direction, entretien, transport), et d'ateliers de production fabriquant chacun un produit (fig.6).
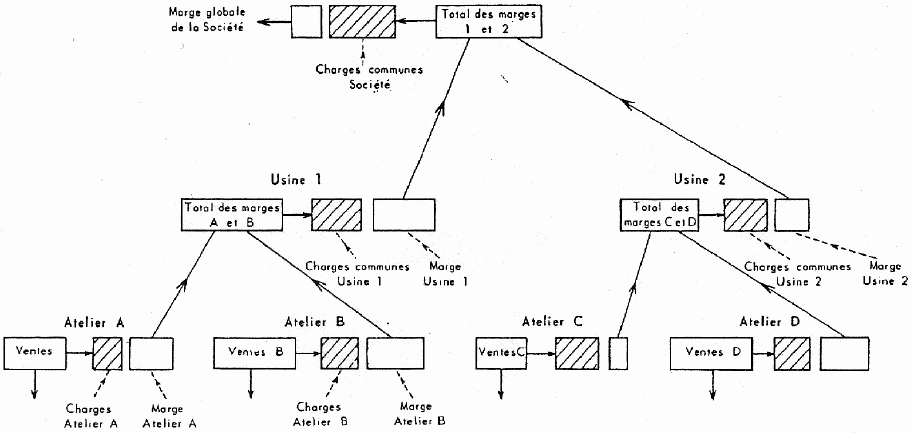
Figure 6
Pour la production de chaque atelier, on calculera un coût de revient atelier qui ne comprendra que ses charges propres, et ses consommations d'entretien et de transports : en comparant au prix de vente, on obtiendra une marge au niveau de l'atelier. (On désigne souvent par marge brute, la différence entre un prix de vente et coût de revient complet).
Puis, au niveau de l'usine, seront ajoutées aux charges des ateliers les charges non ventilées, par exemple les frais de direction, et l'on obtiendra une marge globale usine, sans se soucier d'un éventuel coût de revient usine de chaque produit.
Les marges des usines seront ajoutées au niveau du siège social, où on leur retranchera enfin les charges communes, pour obtenir le résultat global.
Par exemple, le coût de revient partiel du produit A pourra se présenter ainsi :
salaires directs atelier A : 100 achats atelier A : 80 amortissements des machines atelier A : 20 ____ 200
chiffre qui pourra être mis en regard du prix de vente, par exemple 350, la marge de 150 fournissant une appréciation de la contribution de l'atelier A à la couverture des charges de l'usine 1 et du siège social de la société.
Toutefois, ce coût comptable comporte des frais fixes, en l'occurrence des amortissements de machines. Si la question posée concerne une variation de production qui ne met pas en cause le parc de machines, mais seulement les salaires et les achats, il convient de ne retenir que ces deux termes, soit 100 + 80 = 180,c'est-à-dire uniquement les charges directes et variables. Cette dernière méthode porte en anglais le nom de "direct costing", nom assez malencontreux d'ailleurs car les charges directes mais fixes n'y sont pas incluses.
On voit que les coûts de revient ateliers ainsi définis se rapprocheraient a priori d'un coût marginal et à ce titre ils inspirent plus confiance à l'économiste qu'un coût de revient complet. En fait, cette confiance est illusoire, car le concept de coût variable est difficile à mettre en oeuvre : à quel terme considère-t-on la variabilité des frais en cause et de quelle modification de la production s'agit-il ? Dans quelle mesure les salaires peuvent-ils être considérés comme des charges variables ? Nous reviendrons sur ces points à propos du coût marginal au chapitre VI.
On peut résumer les développements précédents en remarquant que deux choix principaux sont offerts pour le calcul des coûts de revient :
On note que ces deux choix se combinent (figure 7).
| Réel | Standard | |
|---|---|---|
| Complet | X | X |
| Partiel | X | X |
Figure 7
On peut être tenté d'établir une hiérarchie entre ces quatre possibilités, par ordre de raffinement croissant. Mais il convient d'être prudent dans de tels jugements, d'une part en raison du fait que la précision du résultat final n'est jamais meilleure que celle des données de base, d'autre part en raison du caractère très variable de l'emploi effectif par les gestionnaires des données comptables, enfin en raison du coût propre du recueil et de l'élaboration des données, non seulement en dépenses monétaires, mais en efforts, tensions, conflits que la mesure de l'activité humaine entraîne toujours peu ou prou.
Il ne saurait être question d'entrer ici dans un exposé de technique comptable, mais seulement de noter une fois de plus que l'évaluation du coût d'un bien ou d'un service donné à l'aide d'un coût comptable peut donner des chiffres divers selon que l'on use de l'une ou l'autre des modalités de calcul énumérées ci-dessus, qui recouvrent chacune de nombreuses variantes.
Si sophistiqué que soit un calcul de coût comptable, il ne peut servir d'évaluation du coût d'un bien en tant qu'attribut du bien considéré.
L'exemple du coût de revient d'un objet manufacturé pourra en fournir une illustration.
Supposons que cet objet soit fabriqué dans un atelier où tous les ouvriers sont payés mensuellement, et qui n'est pas tout à fait saturé au moment où l'on se pose la question. Supposons de plus que l'entretien de cet atelier soit assuré de façon périodique, indépendamment des fluctuations de l'activité à court terme. Dans ces conditions, il est probable que les dépenses effectives entraînées par la production de cet objet se réduiront à d'éventuels achats de matières premières.
A l'inverse, il peut se faire que, pour une différence
de charge minime de l'atelier, la production de cet objet entraîne
le paiement d'heures supplémentaires
aux salariés, voire la location temporaire de matériel.
Dans le premier cas, le coût de la décision de produire est inférieur à n'importe quel coût de revient ; dans le second cas, il est très probable qu'il dépasse de beaucoup toute évaluation comptable moyenne.
Le calcul économique, on le sait, donne à ce genre de problèmes une formulation théorique sous les noms de coûts à court et long terme.
La valeur d'un coût de revient, quel que soit le principe du calcul, dépend de la période sur laquelle il est calculé. Le coût de revient des 10 derniers objets fabriqués n'a pas de raison d'être égal au dixième de celui des 100 derniers ou au centième de celui des 1 000 derniers objets fabriqués.
On peut donner de ce fait une illustration graphique (figure 8). Si l'on représente les charges comptables cumulées en fonction de la production cumulée au cours d'une année, le coût de revient unitaire annuel est représenté par la pente de droite OP, le coût de revient des(N-N1) dernières unités par la pente de la droite QP, celui des (N-N2) dernières unités par la pente de la droite RP. L'allure de la courbe elle-même peut s'expliquer par exemple comme le résultat d'un sous-emploi en début d'année, suivi d'une période de saturation de moyens de production puis par une nouvelle baisse d'activité assortie d'une hausse des prix.
Il faut noter en outre que la forme de la courbe de la figure 8 est modifiée par tout changement de modalité de ventilation dans le temps.
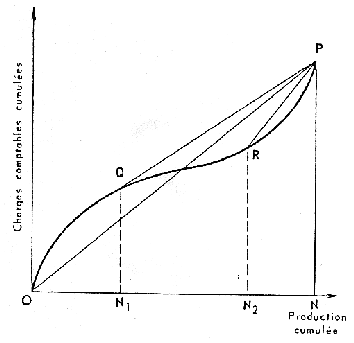
Figure 8