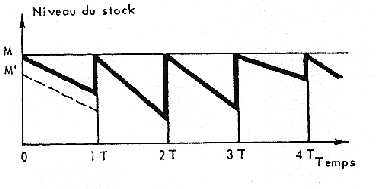
Figure 9 - gestion à la période économique
* * * * *
L'application de la définition générale des coûts aux éléments les plus courants de l'activité industrielle, comme le travail, les fournitures et les transports, montre à quelles erreurs les coûts de revient que l'on calcule de façon usuelle peuvent conduire sur le coût des décisions ou des événements où ces éléments interviennent.
Cette définition permet aussi de fournir des évaluations d'éléments de choix qui ne font pas l'objet d'évaluations comptables, comme des coûts de défaillance de matériel ou des coûts de rupture de stock.
Une conséquence de la définition générale est qu'il n'y a pas de valeur incontestable du coût d'une décision, puisque ce coût dépend de l'observateur, des deux scénarios qu'il compare, et des éléments quantifiables ou non qu'il prend en compte.
Aussi devrons-nous nous borner, dans les exemples qui suivent, à dénoncer quelques erreurs couramment commises, et à suggérer des raisonnements corrects.
Dans une deuxième partie, nous traiterons de deux exemples de coûts industriels pour lesquels la comptabilité est muette.
Dans une troisième partie enfin, nous verrons sur l'exemple de la valeur du temps jusqu'où l'on peut tenter de quantifier des éléments qualitatifs.
La plupart des décisions en univers industriel font intervenir des dépenses de main-d'oeuvre, de fournitures et de transports. Le danger de l'évaluation des coûts correspondants est qu'il n'est nullement intuitif que ces coûts posent des problèmes, puisque toute comptabilité, même sommaire, donne l'apparence de les fournir. Or, les chiffres ainsi trouvés peuvent être tout à fait inadéquats.
Comme la définition des coûts le suggère, il convient de distinguer plusieurs cas selon la nature de la décision en cause.
a) la décision fait intervenir des emplois complets
En théorie économique classique, le travail humain est le facteur de coût que l'on cite usuellement en premier.
En tant que ressource rare, il est considéré comme d'autant mieux utilisé qu'on en consomme moins, toutes choses égales par ailleurs.
Les problèmes d'aménagement du territoire et de chômage qui se posent avec plus ou moins d'acuité depuis quelques décennies dans tous les pays ont altéré la simplicité de cette vision. On a vu ainsi se développer le thème du "coût de création d'un emploi", expression qui désigne l'investissement nécessaire pour offrir un nouveau poste de travail. Il est clair que, du point de vue de l'observateur qui fait usage de cette expression, un emploi de plus est un gain.
Il n'en reste pas moins que pour l'observateur qu'implique le compte de résultat d'une entreprise, un emploi reste une dépense, et c'est de ce point de vue que nous nous placerons dans la suite du présent paragraphe.
Il faut savoir qu'au salaire brut, somme directement due au salarié, s'ajoutent en comptabilité des imputations nombreuses, variables d'une entreprise à une autre, que l'on englobe sous le nom de charges connexes (on dit aussi charges annexes).
Il existe deux sortes de charges connexes :
L'importance de l'analyse des charges connexes tient au fait qu'elles peuvent représenter un montant de même ordre que le salaire brut, mais qu'elles doivent intervenir plus ou moins selon les décisions considérées.
Les prélèvements fiscaux et parafiscaux ne posent pas de problème difficile, bien que leur calcul soit parfois compliqué, puisqu'ils représentent des dépenses effectives de l'entreprise, au même titre que le salaire direct. Toutefois, ce ne serait pas forcément le cas si l'entreprise gérait elle-même des organismes autonomes d eSécurité Sociale.
Les congés payés sont généralement ventilés mensuellement, en comptabilité, de manière que les comptes des semaines de congés ne dénoncent pas un déficit artificiel. Mais il faut prendre garde au fait que les droits à congés, ainsi que les primes diverses, ne sont pas nécessairement proportionnels au temps de travail.
Le logement, le transport et la formation professionnelle sont trois exemples courants de services fournis par l'entreprise elle-même à ses employés. Chacun de ces services entraîne des dépenses globales de main-d'oeuvre, d'équipement et de fournitures, que la comptabilité ventile souvent sur tous les salaires, par exemple au prorata du salaire brut. Mais étant donné le caractère fortement discontinu des dépenses effectives correspondantes (construction ou vente d'une maison, établissement ou suppression d'une ligne d'autocars, création ou suppression d'un cours d'apprentissage ou de recyclage) chaque décision d'augmentation ou de diminution de personnel entraîne des dépenses qui n'ont aucune raison d'être proportionnelles aux salaires bruts en cause.
Les caisses de retraite posent un problème particulier. Il existe en effet deux systèmes de retraites:
A effectif et salaires constants, les deux systèmes sont équivalents. En revanche, le deuxième est avantageux pour l'entreprise lorsque l'effectif croît, désavantageux dans le cas contraire.
Bien entendu, le problème ne se pose que pour les caisses de retraite gérées par l'entreprise elle-même. Sinon, les versements à une caisse extérieure se présentent comme des dépenses effectives.
L'intervention des charges connexes rend délicat le calcul comptable de l'économie procurée par une diminution de personnel. On distingue les charges éludables, qui disparaissent dès que l'agent quitte l'entreprise (par exemple, le salaire brut et les congés payés) et les charges inéludables, ou éludables à terme, qui ne disparaîtront qu'après un délai plus ou moins long (par exemple, le logement et le formation professionnelle). Les analyses qui précèdent montrent qu'il n'est possible de faire des calculs corrects qu'en définissant explicitement l'échéancier des décisions en cause.
Pour terminer sur ce point, signalons une conséquence curieuse de l'imputation comptable des charges connexes. Considérons, pour simplifier, une entreprise fabriquant un produit unique. Le coût de revient de ce produit pourra se présenter sous deux formes :
coût de revient professionnel (par natures) :
salaires 100 charges connexes sur les salaires 60 autres frais 200 ___ total: 360
coût de revient technique (par fonctions) :
salaires 90
charges connexes sur les salaires 80
autres frais 190
___
total: 360
La raison de cette différence est contenue dans la dénomination de ces deux coûts de revient (par natures et par fonctions). Le premier englobe tous les salaires versés par l'entreprise, y compris ceux des agents des services du personnel (transport, logement, formation professionnelle, etc.), et les charges connexes ne comprennent que les versements à des organismes extérieurs. Dans le second, au contraire, l'ensemble des dépenses du service du personnel est inclus dans les charges connexes : la rubrique salaires ne contient que les rémunérations des agents directement employés à des tâches de production.
Ces deux coûts de revient ont chacun leur usage propre en comptabilité, mais nous les avons cités pour mettre en garde, une fois de plus, contre un usage irréfléchi des données comptables.
b) la décision ne fait intervenir que des heures de travail
L'heure de travail est une unité d'oeuvre fréquemment employée dans les devis et les factures. Cette pratique est constante dans les métiers où domine le travail manuel, mais on peut la rencontrer aussi dans les tarifs de consultation de certains cabinets d'ingénieurs-conseils par exemple. On est souvent étonné de constater que le prix de l'heure ainsi utilisé excède d'un coefficient souvent élevé (trois, cinq ou dix) le salaire horaire du professionnel concerné. Cela s'explique évidemment par le fait que l'entreprise en cause définit sa production en heures d'intervention et vend ces heures en fonction de leur coût de revient complet, qui inclut toutes les dépenses autres que la rémunération du professionnel en cause.
Plaçons-nous maintenant du point de vue de l'entreprise qui s'interroge sur le coût d'une augmentation ou d'une diminution du temps de travail de son propre personnel.
Une comptabilité analytique fournit généralement, pour un agent déterminé, un coût de revient réel ou standard de son heure de travail, et l'on est soumis à la tentation de prendre ce chiffre pour évaluer le coût d'une décision qui modifie la charge de main-d'oeuvre.
Ici encore, il convient d'analyser soigneusement la nature de cette décision avant de se prononcer. Compte tenu de la grande variété des cas de figures concevables, nous nous bornerons à quelques indications générales.
Notons tout d'abord que la main-d'oeuvre est payée principalement de trois manières :
Par ailleurs, les heures de travail en cause pourront venir en augmentation ou en diminution par rapport au scénario de référence, et cette modification pourra être temporaire ou durable.
Toutes les combinaisons de modalités de paiement des salaires, et de natures de décision, peuvent conduire à des réponses différentes, pour un même nombre d'heures.
Par exemple, une augmentation occasionnelle de travail demandée à un mensuel pourra ne rien coûter à l'entreprise en terme de salaire, ou au contraire être payée en heures supplémentaires ; elle pourra être demandée à un travailleur temporaire extérieur ou être obtenue par une augmentation provisoire du rendement, etc.
Si la même augmentation de travail doit être permanente, il faudra sans doute envisager une embauche supplémentaire.
La question se pose alors du coût à imputer à cette embauche. Il se peut que, dans une entreprise importante, il y ait d'autres demandes d'heures de travail pour le même emploi, qui permettent d'employer à plein le nouvel agent. Mais il convient alors de se demander si l'embauche considérée est exigée de toute manière par le projet, auquel cas il faut la lui imputer entièrement, ou si elle est subordonnée à la possibilité d'utiliser cet agent à d'autres tâches, auquel cas toute ventilation est discutable, et l'on doit explicitement inclure dans le coût de la décision l'ensemble des tâches concernées.
Le problème d'une diminution de travail est loin d'être symétrique de celui de l'augmentation, car il est bien plus difficile de diminuer un salaire que l'augmenter, de licencier que d'embaucher. Un chef d'entreprise disait un jour : "je suis étonné de constater que les nombreux tiers ou quarts d'employés dont l'économie m'était annoncée à chaque réorganisation n'ont jamais conduit à l'économie d'un employé entier". Cette remarque n'est qu'une boutade, et il est tout aussi déraisonnable de considérer les dépenses de salaires comme fatales, que de prévoir une économie exactement proportionnelle aux heures dégagées. Seule une étude réaliste des conséquences matérielles et humaines des décisions permet de répondre.
Les fournitures (matières premières, pièces détachées, etc.) transitent généralement par un stock avant d'être utilisées en fabrication, et l'on se pose le problème du coût de la décision de prélever de ce stock une unité supplémentaire.
Si toutes les unités de stock ont été achetées au même prix la comptabilité retient évidemment ce prix, majoré forfaitairement de frais de stockage et de manutention, comme imputation au coût de revient.
Si, par contre, le stock est composé d'unités achetées à des prix différents, le calcul du coût de revient pose un problème que la comptabilité résout de l'une des trois manières suivantes :
C'est la troisième méthode qui est exigée en France par le fisc, et donc recommandée par le Plan comptable général, mais les deux autres se rencontrent en comptabilité analytique.
Par exemple, imaginons un stock schématique, composé, dans cet ordre, de :
10 pièces achetées 30 F 15 piècesachetées 20 F 15 pièces achetées 10 F Avec la méthode 1, la pièce sortie est comptée : 30 F Avec la méthode 2, la pièce est comptée : 10 F Avec la méthode 3, elle est comptée : 10 x 30 + 15 x 20 + 15 x 10 ____________________________ = 18,75 F 10 + 15 + 15
Il apparaît ainsi que les trois conventions comptables conduisent à trois réponses différentes.
En fait, pour évaluer le coût de la décision de sortir une pièce, il faut appliquer la définition générale, c'est-à-dire comparer les dépenses effectives dans le cas où l'on sort cette pièce, et dans le cas où on ne la sort pas.
Il apparaît alors que l'histoire passée du stock ne joue aucun rôle dans cette évaluation. En effet, il convient de se demander en quoi la décision de sortir une pièce va modifier les dépenses futures, et dépend par conséquent du mode de gestion adopté pour ce stock.
Montrons comment cette évaluation peut être faite dans deux cas particuliers :
a) gestion à la période économique : dans ce mode de gestion, on passe commande à période fixe d'une quantité variable en fonction de l'état du stock à ce moment. Le fait de prendre une pièce de plus aura pour effet de majorer d'une unité la commande suivante, et par conséquent le coût de la décision est le prix d'achat de cette pièce à ce moment (fig. 9).

Figure 9 - gestion à la période économique
b) gestion à la quantité économique : dans ce cas, au contraire, la quantité commandée est constante, et c'est la date de la commande qui varie. Par conséquent, le fait de prendre une pièce de plus aura pour effet de rapprocher la date de la prochaine commande et de toutes les suivantes (fig. 10).
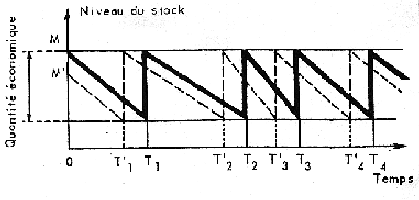
Figure 10 - gestion à la quantité économique
Le résultat n'a aucune raison d'être le même dans les deux cas, puisque dans le premier, il ne fait intervenir que le prix du bien lors de la prochaine commande, et dans le second, la chronique infinie de tous les prix d'achat futurs.
Bien entendu, il n'y a pas de raison pour qu'un stock soit nécessairement géré de l'une ou de l'autre manière, ni pour que le mode de gestion en soit pas modifié par la décision en cause.
Les transports sont une source inépuisable de problèmes d'évaluation des coûts, pour la raison que les dépenses effectives du transporteur sont marquées de fortes discontinuités (un camion, un train, un avion, un navire de plus ou de moins) entre lesquelles elles varient peu tant que ces moyens ne sont pas saturés, alors que les prix varient le plus souvent proportionnellement à une quantité et à une distance, avec ou sans terme fixe. C'est ainsi que l'on considère couramment, en matière de marchandises, une unité d'oeuvre appelée TKU (tonne x km utile), et en matière de transport de personne, le km x voyageur.
A cet égard, la littérature économique est souvent revenue sur le problème dit "du voyageur de Calais", qui s'énonce de la façon suivante : quel est le coût de l'embarquement d'un voyageur supplémentaire qui se présente inopinément juste au moment du départ d'un train ?
La difficulté du problème réside dans le fait que la dépense supplémentaire entraînée par l'embarquement de ce passager peut varier énormément selon les circonstances : si le train n'est pas complet, un voyageur de plus ne compte presque pas ; c'est déjà moins vrai si le train est plein ; il faudrait alors ajouter un wagon, à moins que la charge maximum du train ne soit atteinte, auquel cas il faudrait faire partir un autre convoi, à moins que la voie ferrée ne soit saturée, auquel cas il faudrait envisager son doublement.
Les économistes ont imaginé des solutions variées pour résoudre ce problème. Nous en résumerons deux :
Il convient de s'interroger sur la raison pour laquelle ce problème a tant inquiété les économistes. Après tout, qu'importe le coût du voyageur de Calais ?
La raison de cet intérêt est liée, sans aucun doute, au besoin théorique et pratique de justifier le prix du billet ; besoin théorique, dans la mesure où le calcul économique classique est issu de la théorie des situations de Pareto, dans laquelle les fonctions de dépenses sont continues et dérivables, et les prix égaux, à l'équilibre, aux coûts marginaux à court et long terme ; besoin pratique, dans la mesure où les transports publics, compte tenu de leur vocation à servir l'intérêt général, doivent être tarifés à un juste prix.
En fait, le prix du billet du voyageur de Calais n'a aucune raison d'avoir un rapport direct avec un coût quelconque. C'est un paramètre dans un problème à composantes multiples, parmi lesquelles interviennent l'élasticité de la demande de transports, la concurrence des autres modes, les relations entre le budget de la compagnie des chemins de fer et le budget de l'État, les transferts sociaux,etc. On peut noter à ce sujet que c'est au moment où ses dépenses effectives sont maximum, à l'occasion des départs en vacances, que la S.N.C.F. consent le plus de réductions, avec les billets de congés payés et les billets de groupes, ce qu'elle tend à compenser en différenciant les tarifs selon les heures.
Si l'on renonce à la recherche du juste prix, le calcul du coût perd de son importance ; il n'est pas interdit pour autant de l'entreprendre, mais il ne prend un sens qu'au titre de coût d'un événement ou d'une décision qu'il convient donc de définir.
Si l'événement en question est l'embarquement d'un voyageur isolé, il est hors de doute que le coût est toujours à peu près nul du point de vue de la compagnie.
Il est alors intéressant de chercher à quelles décisions peuvent correspondre les deux solutions proposées par les économistes et résumées ci-dessus.
La première correspond à l'hypothèse d'une demande de transport croissante, et à la mise en service de moyens de transports supplémentaires au fur et à mesure que la demande l'exige.
La seconde solution repose sur une hypothèse tout à fait différente. On imagine cette fois-ci une demande constante en moyenne, mais irrégulière ; toutefois, cette irrégularité est régie par une loi de distribution connue, ce qui permet de fixer le nombre de trains et de wagons nécessaires pour assurer au voyageur une probabilité définie de trouver une place.
Deux remarques s'imposent concernant ces deux calculs : leur incompatibilité et leur caractère arbitraire.
Le premier calcul exige une demande déterministe et croissante, le second exige une demande aléatoire et de distribution stable. Le premier calcul suppose que l'on augmente les équipements pour satisfaire complètement la demande, le second suppose que l'on maintient les équipements pour satisfaire une proportion statistiquement constante de la demande, sans chercher à satisfaire celle-ci entièrement.
Autrement dit, ces deux calculs de coût ne sont pas en opposition, ils traitent en fait de deux problèmes différents. Notons aussi qu'ils perdent l'un et l'autre leur validité si l'on change l'une quelconque de leurs hypothèses. Si dans le premier cas, la demande est constante, il ne reste plus que des dépenses d'exploitation et d'entretien, que l'on peut ventiler sur les voyageurs d'une infinité de manières. Il en va de même dans le second cas si l'on remet en cause la définition de la population concernée par le transport pour Calais.
L'arbitraire ne porte donc pas seulement sur les événements et les décisions qui expliquent les dépenses, il porte aussi sur la ventilation de ces dépenses entre les voyageurs. Après tout, le voyageur de Calais peut fort bien proclamer, dans un cas comme dans l'autre, que le fait qu'il prenne ou non le train ne change pas les dépenses de la compagnie, quelle que soit par ailleurs la politique de cette dernière. A quoi la compagnie répondrait que si elle prenait ce genre de raisonnement en considération, personne ne paierait son voyage.
L'évaluation des coûts est d'un maigre secours pour permettre de trancher le débat tarifaire. Sa contribution se réduit à cette conclusion : le coût du voyageur de Calais n'existe pas, seules existent une infinité de décisions possibles qui n'ont en commun que le fait de transporter ce voyageur particulier, décisions dont le coût peut être infiniment varié.
Toute décision visant à se prémunir contre des aléas associe implicitement ou explicitement un coût aux événements que l'on veut éviter. Deux exemples, familiers en calcul économique et en recherche opérationnelle, s'imposent à l'esprit : les stocks de sécurité, et l'entretien préventif du matériel.
On sait qu'un stock comporte deux aspects.
D'une part, il sert de régulateur entre des ressources et des besoins de débits instantanés différents : par exemple, il peut se faire que l'on consomme exactement une pièce par jour, mais que ces pièces soient livrées par caisses de 100. On a ainsi en moyenne 50 pièces en stock, sans intervention d'aucun aléa.
Mais, d'autre part, ce stock peut être majoré d'un certain montant destiné à faire face à des irrégularités du débit entrant (aléas sur les délais de livraison, par exemple) ou du débit sortant (aléas sur la consommation). On appelle ce supplément le stock de sécurité.
L'acquisition et la conservation de ce stock de sécurité entraînent des dépenses effectives, dépenses que l'on consent pour éviter les conséquences des ruptures de stock. A supposer que l'on puisse associer à chaque niveau du stock de sécurité l'espérance mathématique du nombre de ruptures, sur une période donnée, on doit choisir le niveau de telle manière que le total du coût du stock de sécurité et du coût des ruptures soit minimal. Cela suppose donc que l'on dispose d'une évaluation des coûts de rupture de stock.
Il est bien évident que la comptabilité ne saurait posséder aucune rubrique de cette nature. En revanche, la définition générale des coûts permet de poser le problème, sinon de toujours le résoudre.
Le coût de rupture d'un stock est l'échéancier de toutes les conséquences entraînées par cette rupture. Elles peuvent être variées.
Considérons par exemple le stock de pièces de rechange d'un atelier d'entretien. Si une pièce manque au moment où un matériel vient en réparation, on pourra peut-être réparer la pièce endommagée au lieu de la changer, ou usiner une pièce de remplacement, ou aller chercher d'urgence la pièce manquante chez son fabricant, ou simplement attendre la prochaine livraison, etc. Ces différentes décisions ne sont pas équivalentes pour l'atelier d'entretien, ni pour l'utilisateur de la machine. Apparaît alors l'importance du point de vue de l'observateur. Il se peut fort bien que la décision d'attendre la prochaine livraison soit désastreuse pour son client, qui a un besoin urgent de cette machine. Selon l'ampleur du domaine pris en compte pour évaluer le coût de cette rupture, on pourra ainsi être conduit à des valeurs différentes du stock de sécurité.
Notons au passage qu'une telle interaction indique encore une fois le danger possible d'une décentralisation des responsabilités par le biais des imputations comptables. On pourrait imaginer par exemple que l'atelier utilisateur de la machine, ne pouvant obtenir une sécurité suffisante de la part de l'atelier de réparation, fasse l'acquisition d'une machine de secours, constituant ainsi un stock de sécurité sans doute plus coûteux que le stock de pièces de rechange dont l'atelier d'entretien devrait disposer. La logique comptable fait pourtant que c'est à l'atelier utilisateur que cette deuxième machine sera imputée, et non pas à l'atelier d'entretien défaillant.
Le cas du stock d'un commerçant est souvent encore plus difficile à quantifier, car l'évaluation du coût de rupture ne peut être faite qu'en imaginant le comportement des clients devant cette rupture. S'il s'agit des ménagères clientes d'un droguiste, peut être l'abandonneront-elles définitivement en ne trouvant pas leur lessive favorite, mais peut être achèteront-elles une marque concurrente, à laquelle elles resteront éventuellement attachées par la suite. Il est à remarquer qu'ici encore, le point de vue de l'observateur jour un rôle dominant ; si c'est la deuxième éventualité qui se produit, le coût de rupture peut être négligeable pour le commerçant, mais certes pas pour le fabricant de la lessive absente.
La difficulté de l'évaluation des coûts de rupture de stocks est telle que les gestionnaires lui substituent souvent un paramètre plus intuitif : le taux de service, exprimé en pourcentage. Un taux de service de 95 % signifie que l'on admet qu'une demande arrivant à un instant quelconque sera satisfaite dans 95 % des cas. Il est souvent utile de calculer le coût de rupture qu'implique un tel choix, pour vérifier qu'il n'est pas dangereusement sur- ou sous-estimé.
On peut distinguer deux catégories de dépenses d'entretien du matériel : les réparations, et l'entretien préventif. Dans le deuxième cas, on consent à affronter les dépenses d'entretien connues, afin d'éviter des coûts de défaillances aléatoires. Comme dans le cas des stocks de sécurité, on vise à minimiser le total des coûts en cause.
L'analogie va d'ailleurs plus loin, car il se produit souvent que les deux problèmes soient liés. Imaginons que la machine citée dans le cas précédent fasse partie d'une chaîne d'usinage. Il est alors possible de constituer un stock des produits de cette machine, qui peut permettre à la machine suivante de continuer à travailler un certain temps pendant une réparation.
On est donc conduit à des discussions comparables à celles du paragraphe précédent, à cette différence près que l'information technique de base, d'ailleurs difficile à obtenir dans bien des cas, est cette fois l'influence de l'entretien préventif sur les probabilités de pannes.
Une autre différence concerne les responsabilités en cause. Nous avons vu, dans le cas des stocks de sécurité, que lorsque le gestionnaire du stock n'est pas la principale victime des ruptures éventuelles, il y a un danger de biais dans l'estimation du stock de sécurité. Néanmoins, cette situation n'est pas la plus fréquente.
En matière d'entretien, en revanche, le service chargé des interventions importantes est très souvent une véritable usine dans l'usine, et jugé comme telle sur des critères comptables qui lui sont propres. C'était notamment le cas pour l'exemple réel dont l'illustration suivante a été tirée.
Le problème de coût de défaillance concernait le matériel d'abattage d'une mine de charbon.
Supposons que l'on soit arrivé à montrer que l'arrêt accidentel d'une machine déterminée (rabot, haveuse, convoyeur blindé, par exemple) conduit, s'il se produit pendant le poste d'abattage, à une diminution de production au cours de ce poste évaluée à T tonnes de charbon en moyenne (nous n'insistons pas sur cette évaluation, mais comme la production d'un chantier est normalement variable, on devine qu'une analyse statistique approfondie est nécessaire).
Appliquons la définition générale : le coût de cette défaillance sera obtenu en comparant toutes les dépenses effectives dans la situation 1, où elle ne se serait pas produite, et la situation 2, où elle s'est produite.
Cette situation 2 est principalement caractérisée, au jour 0 de la panne, par :
Les autres dépenses n'ont pas de raison d'avoir beaucoup varié, puisque cette diminution de production était inopinée : tout le personnel de la mine a été payé de la même manière, et le matériel de desserte, d'extraction, etc... est resté en service. Si, de plus, la durée de l'arrêt a été courte, il n'a pas été possible d'employer le personnel du chantier à d'autres tâches. Tout au plus peut-on penser que quelques frais de lavage du charbon (consommation d'énergie) ont diminué, somme qui peut être considérée comme négligeable.
En revanche, cette défaillance a des conséquences sur l'avenir.
On peut penser que les T tonnes ne sont pas vraiment perdues, puisqu'elles seront finalement exploitées. Mais seront-elles exploitées le lendemain de la défaillance ? Si l'on suppose, comme c'est normalement le cas, que les moyens de la mine sont saturés en probabilité, il n'y a pas de raisons pour qu'une défaillance au jour J s'accompagne d'une augmentation de production au jour J+ 1. En fait, il faut admettre que, dans ces conditions, la diminution de production aura pour effet de prolonger la vie de la mine au moment de sa fermeture dans n années, si tant est que l'épuisement des ressources soit le critère du choix de la date de fermeture, ce que nous admettrons pour l'instant.
Mais la récupération de ces T tonnes suppose que l'on maintienne la mine en activité pour les exploiter, et entraîne donc des dépenses effectives D.
Le calcul du coût de défaillance se présente alors comme suit :
différence entre scénario 1 (pas de défaillance) etscénario 2 (défaillance) :
Dans bien des cas, les dépenses et recettes situées dans n années joueront un rôle négligeable devant les autres termes, non seulement à cause de l'éloignement dans le temps, mais aussi parce que la valeur marchand des T tonnes à cette date sera amputée des dépenses D nécessaires pour les produire, alors que la perte de ce même tonnage au moment de la défaillance représente la seule valeur marchande de ces tonnes. Enfin, si la date de fermeture est choisie selon d'autres critères que l'épuisement des ressources, les T tonnes ne seront jamais récupérées.
Le coût de la défaillance est alors la somme des dépenses effectives de réparation et de la valeur marchande des tonnes perdues.
Il est à remarquer que ce résultat est conforme au bon sens, et l'on peut s'étonner qu'il ait fallu une analyse aussi poussée pour y parvenir. Mais il faut prendre garde au fait que, dans la plupart des problèmes d'évaluation des coûts, le bon sens suggère bien souvent des réponses erronées, et qu'il convient de se méfier des raccourcis de raisonnement.
Il faut noter que, dans le cas considéré, le coût évalué ci-dessus est étroitement lié aux nombreuses hypothèses que nous avons introduites dans le calcul. Il serait remis en cause si, par exemple, la mine s'assignait pour objectif de réaliser une production mensuelle constante, en pratiquant éventuellement des heures supplémentaires, ou si la durée de la défaillance était suffisamment longue pour permettre d'employer la main-d'oeuvre dans d'autres chantiers.
Quoi qu'il en soit, le calcul ci-dessus appliqué à l'ensemble de l'entreprise a montré que les économies que pouvait faire le service d'entretien en laissant des pertes de tonnage se produire pouvaient résulter d'un calcul logique au niveau de cet atelier, mais mauvais pour l'entreprise dans son ensemble.
Les coûts de défaillance ne sont pas mesurés par la comptabilité, mais on peut imaginer, au moins théoriquement, des évaluations objectives fondées sur des flux monétaires. Il n'en va plus de même pour l'évaluation des coûts touchant, non pas seulement à l'économie, mais à d'autres aspects de la vie en société. L'exemple le plus frappant est le coût d'une vie humaine. Les dépenses consenties pour améliorer la sécurité des personnes sont souvent justifiées par de telles évaluations ; il en va de même pour les dommages et intérêts attribués aux ayants droit des victimes d'accidents.
Très similaire est le problème de la valeur du temps, qui se pose dans la plupart des calculs économiques touchant aux transports urbains et interurbains de personnes. Quelle valeur économique faut-il accorder au fait que des utilisateurs d'une liaison bénéficient d'une réduction de leur temps de parcours grâce à un investissement (accélération des véhicules, augmentation des fréquences, liaison nouvelle plus rapide, etc.) ? Ce sujet a fait depuis trente ans l'objet de nombreux travaux et de vives controverses. Nous allons montrer que la définition générale des coûts apporte quelque lumière dans ces débats.
Pour évaluer la valeur du temps des usagers, la méthode la plus employée consiste à étudier les comportements d'une population qui se rend régulièrement d'un point A à un point B (par exemple domicile-travail) et qui a pour cela le choix entre deux moyens de transport tel que le plus rapide soit aussi le plus cher.
En postulant que chaque usager arbitre entre son temps et sa dépense en fonction d'une valeurmonétaire des minutes gagnées ou perdues, on cherche statistiquement quelle valeur de ce rapport explique le mieux les choix opérés. On distingue habituellement les catégories socio-professionnelles et l'on constate, comme le bon sens le suggère, que le temps des riches vaut plus cher que le temps des pauvres.
On multiplie alors le temps gagné par la valeur du temps et par les effectifs concernés, et l'on fait entrer les montants obtenus dans les calculs de rentabilité des investissements de transports.
Diverses objections ont été faites à ce mode d'évaluation.
On a fait tout d'abord observer que la valeur du temps issue des calculs précédents est celle que les individus eux-mêmes lui attribuent, c'est-à-dire que le calcul économique suppose que l'investisseur, qui est généralement la puissance publique, souscrive à cette évaluation. Or, elle peut avoir sa propre appréciation de "l'utilité sociale" du temps des divers individus, par exemple leur contribution à la production, ce qui conduira à défavoriser les oisifs.
Une autre remarque, de nature différente, conduit à une remise en cause analogue. On fait observer que, s'il est vrai que la valeur monétaire du temps est une fonction croissante du revenu, il est également bien connu que "l'utilité" psychologique de la monnaie, elle, est une fonction décroissante du revenu. Autrement dit, il n'est pas impossible que si un individu riche évalue une heure de son temps à 100 F, et un individu pauvre à 30 F, cela tienne au fait qu'ils ressentent de telles dépenses de la même manière, c'est-à-dire qu'ils ont en réalité même valeur psychologique du temps.
Cela dit, même dans le cas où l'on peut disposer de mesures significatives de la valeur monétaire du temps, on est réduit à des hypothèses assez vagues, tant sur "l'utilité sociale" du temps des individus que sur "l'utilité" psychologique de la monnaie.
Voyons maintenant l'apport de la définition générale des coûts. La valeur du temps est un élément du coût d'une décision pour un observateur. Quel observateur recensant quels flux ? Les diverses réponses possibles à cette question permettent de classer les opinions précédentes. Si l'observateur est la puissance publique (concept en demeurant difficile à cerner avec précision), on conçoit qu'elle mette par exemple en regard d'une part la contribution économique de chaque individu à la richesse générale et d'autre part l'amputation de cette richesse au titre de l'investissement envisagé. Mais si l'observateur est l'individu choisissant entre deux modes de transport, on ne peut qu'enregistrer une différence de dépenses effectives en temps et en argent, sans préjuger d'une équivalence entre ces deux quantités. Bien entendu, il est fort possible que d'autres facteurs que le temps et l'argent interviennent dans ce choix ; l'échéancier des dépenses effectives doit les recenser.
L'apport de la définition générale des coûts peut paraître bien négatif. Les responsables se trouvent ainsi confrontés à un tableau complexe de tous les enjeux en présence au lieu de l'expression simple de la rentabilité du projet que les méthodes classiques leur proposent. Mais comme toujours en matière de paramètre de gestion, si un simple critère de rentabilité et le choix qu'il suggère donnent satisfaction à toutes les parties concernées, il n'y a pas de raison de le discuter. Si, en revanche il y a désaccord ou conflit,il n'est pas honnête, de la part de ceux à qui le calcul économique classique donne raison, de brandir ce calcul comme une vérité scientifique devant qui tout esprit normal devrait s'incliner.Ce résultat désigne tout au plus une conclusion non invraisemblable, pour reprendre une expression que nous avons déjà employée au chapitre V à propos de l'actualisation. Ceux qui sont en désaccord avec cette conclusion devraient pouvoir en proposer une autre ; à leur charge de démontrer qu'elle est tout aussi non invraisemblable que celle de leurs adversaires. Ce principe est en honneur dans certains pays et dans certaines villes : les adversaires d'un projet de la puissance publique disposent officiellement de moyens d'études pour le combattre.
Mais pour que la négociation porte ses fruits, il est souhaitable que toutes les parties s'accordent sur les faits sous examen, même si elles les interprètent différemment ; le recensement des dépenses effectives prises en compte par les divers observateurs répond à cette préoccupation.
Il est un peu décevant de se rendre compte, en analysant la notion de coût, du fait que l'on en peut concevoir aucun procédé incontestable d'évaluation, ni jamais calculer une valeur qui soit exacte dans l'absolu.
Ainsi, nous n'avons pas pu donner une réponse certaine aux différents problèmes étudiés dans ce chapitre, car nous voulions justement faire sentir que toute apparence de certitude en la matière ne peut être que fallacieuse.
C'est ainsi que ces exemples nous ont permis d'illustrer la définition générale des coûts, en montrant successivement que les données comptables élémentaires ne représentaient que des moyennes, dont chaque cas particulier pouvait s'écarter sensiblement, que les coûts de défaillance pouvaient être diversement appréciés selon la position de l'observateur, et que les aspects qualitatifs des décisions pouvaient jouer un rôle aussi important que les données purement monétaires.
Mais s'il est vrai qu'un coût peut prendre différentes valeurs selon l'observateur, cela ne signifie nullement qu'il peut prendre n'importe quelle valeur. Si les deux décisions en cause sont complètement définies, notamment par la nature des éléments qui y jouent un rôle, ainsi que l'intervalle de temps et le domaine de l'espace pris en compte, le coût est exprimable sans aucune ambiguïté.